
I pentamini nel puzzle di Dudeney
I pentamini sono figure geometriche piane composte da un insieme di cinque quadrati uguali che abbiano a due a due un lato in comune, ossia, in altre parole, cinque quadrati uguali e contigui, uniti per i lati. Il primo ad utilizzare questi pezzi in un problema di ingegno fu il matematico britannico Henry E. Dudeney (in The Canterbury Puzzles and Other Curious Problems, del 1970). Altri matematici, come Martin Gardner e Solomon Golomb, approfondirono i pentamini e le altre figure geometriche simili, studiandone le proprietà e le implicazioni. Nel corso degli anni, i pentamini sono diventati un ottimo passatempo matematico ed un valido strumento didattico: l’uso in matematica ludica porta a stimolare la capacità di osservazione di un pezzo, analizzandone le caratteristiche e confrontandolo con gli altri; di astrazione, immaginando di ruotarlo o traslarlo in modo da incastrarlo con gli altri; di strategia, per ottimizzare gli spostamenti.
Dudeney, in uno dei suoi giochi, propose di ricostruire una scacchiera con il lato lungo 8 quadrati (8×8) con tutti i possibili pentamini che si potevano generare unendo i cinque quadrati. Ma come inserirli? Iniziamo col capire come costruire un pentamino.
Costruiamo un pentamino
Per costruire un pentamino procediamo come segue:
 Disegnamo un quadrato su un foglio di carta a quadretti;
Disegnamo un quadrato su un foglio di carta a quadretti;
scegliamo uno dei quattro lati del quadrato e disegnamo un altro quadrato partendo da questo lato (per esempio il lato in basso); 
ripetiamo l’operazione precedente

(cambiando, per esempio con il lato a destra);
procediamo così per altre tre volte.
Avremo così ottuenuto un pentamino,  costituito da cinque quadrati contigui che hanno un lato in comune a due a due.
costituito da cinque quadrati contigui che hanno un lato in comune a due a due.
E’ evidente che potremo costruire tanti altri pentamini, alcuni dei quali saranno ripetizioni di altri.
Infatti, semplicemente ribaltando un pentamino, riflettendolo o ruotandolo, si otterranno dei pentamini identici. Questa caratteristica apre molti spunti di riflessione sulle proprietà dei pentamini e sulle trasformazioni geometriche (simmetria, traslazione, rotazione) che generano pentamini identici. Quanti possibili pentamini avremo senza contare le ripetizioni?
Dopo qualche minuto di ragionamento e tentativi grafici e pratici, potremo scoprire che le possibili variazioni sono 12. Partiamo da qui per il nostro gioco
Il Puzzle di pentamini
Disegnamo tutti e 12 i nostri modelli.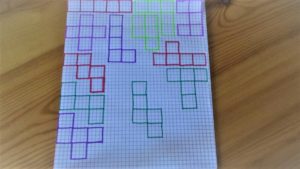
 Ritagliamoli.
Ritagliamoli.
Notiamo subito che alcuni pentamini hanno la capacità di incastrarsi l’un con l’altro. Sfruttando tale proprietà utilizziamoli come pezzi di un puzzle. Iniziamo con qualcosa di semplice: cerchiamo di realizzare un rettangolo con un lato lungo tre quadrati ed uno di cinque quadrati (3×5), utilizzando solo tre pentamini, scelti a piacere.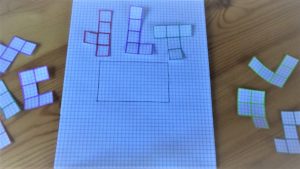 Da qui alcuni interessanti spunti di riflessione sulle possibilità di combinazione e sui limiti di realizzazione. Quanti modi possibili ci sono per realizzare un rettangolo del genere, usando sempre gli stessi tre pezzi? E quanti modi ci sono per ottenere questo rettangolo con altri tre pezzi? Sarebbe possibile ottenere un rettangolo con dimensioni inferiori utilizzando tre pezzi? Perchè?
Da qui alcuni interessanti spunti di riflessione sulle possibilità di combinazione e sui limiti di realizzazione. Quanti modi possibili ci sono per realizzare un rettangolo del genere, usando sempre gli stessi tre pezzi? E quanti modi ci sono per ottenere questo rettangolo con altri tre pezzi? Sarebbe possibile ottenere un rettangolo con dimensioni inferiori utilizzando tre pezzi? Perchè?
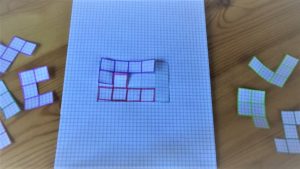
Una possibile soluzione del rettangolo 3×5
La prossima sfida è quella di costruire un quadrato con il lato di cinque quadrati (5×5).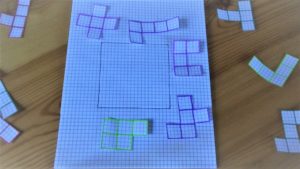

Una possibile soluzione del quadrato 5×5
Questa è una possibile soluzione: ne esistono altre? Possiamo ricoprire un quadrato 5×5 con più di cinque pezzi? E con meno?
E’, inoltre, possibile ricoprire superfici molto più complesse, a forma di un animale o di una pianta; i pentamini possono essere disposti a formare delle lettere dell’alfabeto o, addirittura, delle figure uguali ai pezzi stessi, ingranditi. In questo modo potremo dare libero spazio alla creatività costruendo figure sempre nuove ed elaborate, abbinando alle abilità logico matematiche, quelle grafico creative che questo tipo di attività stimola.

La scacchiera 8×8 con un foro al centro
Infine, il puzzle di Dudeney. Una scacchiera di lato lungo otto quadrati (8×8) in cui inserire tutti i 12 pentamini. Per capire come inserirli, dobbiamo prima chiederci se siano sufficienti. Bastano 12 pentamini per ricoprire la scacchiera 8×8? Ed ecco il motivo per cui Dudeney aggiunse un altro pezzo, quadrato formato da quattro quadrati (tetramino), per completare l’opera. Se il tetramino quadrato fosse posizionato al centro, come inseriremmo tutti gli altri?
La mia proposta
Basandoci sull’ultima scacchiera 8×8, inserendo una zona vuota (foro) al centro di quattro quadrati (al posto del tetramino per intenderci), è possibile creare un campo di gioco in cui due o più partecipanti si confrontino in un gioco collaborativo o competitivo.
Nel gioco competitivo, due giocatori o due squadre di giocatori (ognuno ha la possibilità di inserire un pezzo) inseriscono un pezzo alla volta nella scacchiera 8×8, scelto liberamente. Il primo giocatore, o la prima squadra, che non riesce a collocare un pentamino perde. Se tutti i pezzi sono stati collocati e non ci sono più pezzi da collocare, il giocatore che deve collocare un pezzo perde.
In una variante più semplice ogni giocatore può spostare un pezzo già presente sulla scacchiera ed inserirne uno nuovo. In una variante più complessa, ogni giocatore sceglie il pezzo che dovrà inserire l’altro.
Qual è il numero minimo di mosse che è possibile fare per vincere? E qual’è il numero massimo?
Nella modalità cooperativa, giocabile sempre in due giocatori o due squadre, abbiamo bisogno anche di un timer per un conto alla rovescia. Si stabilisce un tempo di 5 minuti. Ogni giocatore, senza suggerire o parlare con l’altro o gli altri, inserisce un pezzo a scelta. Ogni giocatore può scegliere di mettere un pezzo o spostarne uno già presente sulla scacchiera. Se tutti e 12 pentamini sono stati inseriti sulla scacchiera prima dello scadere del tempo, i giocatori hanno vinto.
In una variante più semplice possiamo aumentare il tempo a disposizione; nella variante più difficile possiamo diminuire il tempo.
Per rispondere alla domanda che ci siamo posti, una soluzione possibile per inserire tutti i 12 pentamini sulla scacchiera 8×8 è questa in figura. Ma è l’unica?

I 12 pentamini nella scacchiera 8×8 con al centro il foro per il tetramino quadrato
Francesco Attanasio
Bibliografia
Come buttarsi dalla torre di Hanoi di Martin Gardner
Sitografia
https://areeweb.polito.it/didattica/polymath/htmlS/probegio/GAMEMATH/Polimini/Polimini.htm
https://ilpiccolofriedrich.blogspot.com/2014/03/pentamini.html
https://www.academia.edu/2601243/Pentamini_Testo_e_immagini_a_cura_di_Francesco_Gilardi
Bellissimo percorso, grazie Francesco!
Grazie mille, sono davvero contento che le piaccia! Continui a seguirmi per altri interessanti articoli!